Combined Rule-Based and Hypothesis-Based Method for Building Model Reconstruction from Photogrammetric Point Clouds
Jan 1, 2021·
 ,
,
,
,
,
,
,
·
0 min read
,
,
,
,
,
,
,
·
0 min read
Linfu Xie
Han Hu
Qing Zhu
Xiaoming Li
Shengjun Tang
You Li
Renzhong Guo
Yeting Zhang
Weixi Wang
Abstract
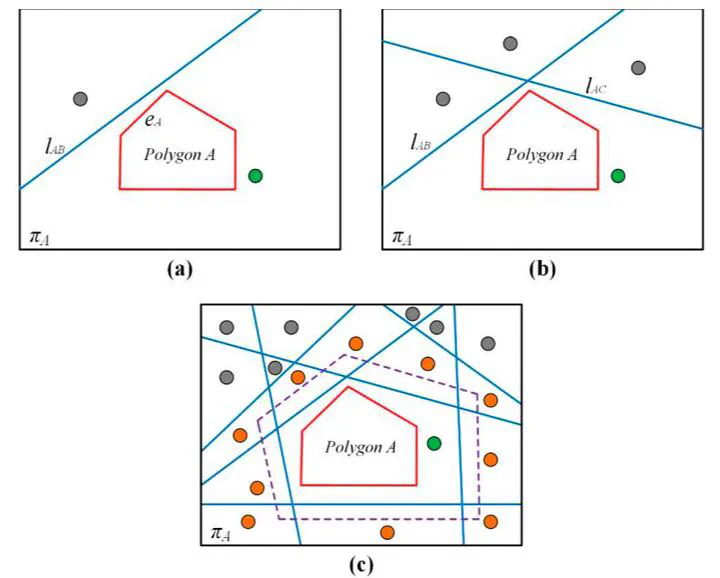
Three-dimensional (3D) building models play an important role in digital cities and have numerous potential applications in environmental studies. In recent years, the photogrammetric point clouds obtained by aerial oblique images have become a major source of data for 3D building reconstruction. Aiming at reconstructing a 3D building model at Level of Detail (LoD) 2 and even LoD3 with preferred geometry accuracy and affordable computation expense, in this paper, we propose a novel method for the efficient reconstruction of building models from the photogrammetric point clouds which combines the rule-based and the hypothesis-based method using a two-stage topological recovery process. Given the point clouds of a single building, planar primitives and their corresponding boundaries are extracted and regularized to obtain abstracted building counters. In the first stage, we take advantage of the regularity and adjacency of the building counters to recover parts of the topological relationships between different primitives. Three constraints, namely pairwise constraint, triplet constraint, and nearby constraint, are utilized to form an initial reconstruction with candidate faces in ambiguous areas. In the second stage, the topologies in ambiguous areas are removed and reconstructed by solving an integer linear optimization problem based on the initial constraints while considering data fitting degree. Experiments using real datasets reveal that compared with state-of-the-art methods, the proposed method can efficiently reconstruct 3D building models in seconds with the geometry accuracy in decimeter level.
Publication
Remote Sensing